Text
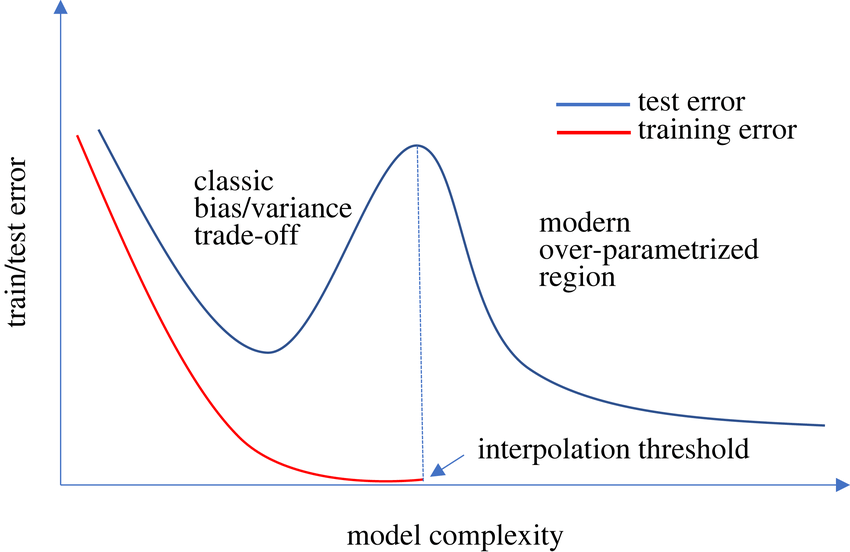
N_{\text{Data}} < N_{\text{Params}}
Tiefes NN kann jede Funktion fitten
-> overfit leicht
-> Generalisierung schwer
Regularisierung reduziert Varianz,
ohne Bias zu erhöhen
-> Modell lernt "einfach" & robust sein
Wieso Regularisieren?
Regularisieren
- reduziert Overfitting
(essentiell bei grossen NN)
- verbessert Generalisierung
- robustere Models & Training
- Balance: Komplexität - Generalisierung

N_{\text{Data}} < N_{\text{Params}}
Regularisieren
- L1 (Lasso):
- kleine Parameter
- Gewichte -> 0 => Feature Auswahl
\text{Loss} + \beta \sum_{i=1}^{n} |\theta_i|
l1_regularization_loss = torch.norm(model.parameters(), 1)Regularisieren
- L1 (Lasso):
- kleine Parameter
- Gewichte -> 0 => Feature Auswahl
- L2 (Ridge):
- kleine, ausgeglichene Parameter
- meistgebrauchte regularisation
\text{Loss} + \beta \sum_{i=1}^{n} |\theta_i|
\text{Loss} + \beta \sum_{i=1}^{n} \theta_i^2
l1_regularization_loss = torch.norm(model.parameters(), 1)optimizer = torch.optim.Adam(model.parameters(), lr=lr, weight_decay=beta)
Regularisieren
- L1 (Lasso):
- kleine Parameter
- Gewichte -> 0 => Feature Auswahl
- L2 (Ridge):
- kleine, ausgeglichene Parameter
- meistgebrauchte regularisation
- Dropout: setzt zufällig Neuronen auf 0
- Modell redundant & robust
\text{Loss} + \beta \sum_{i=1}^{n} |\theta_i|
\text{Loss} + \beta \sum_{i=1}^{n} \theta_i^2
l1_regularization_loss = torch.norm(model.parameters(), 1)optimizer = torch.optim.Adam(model.parameters(), lr=lr, weight_decay=beta)
nn.Dropout(0.2) # 0.2 of neurons set to 0Regularisieren
- L1 (Lasso):
- kleine Parameter
- Gewichte -> 0 => Feature Auswahl
- L2 (Ridge):
- kleine, ausgeglichene Parameter
- meistgebrauchte regularisation
- Dropout: setzt zufällig Neuronen auf 0
- Modell redundant & robust
- Modell redundant & robust
- Batch Normalization: Normalisiert Layer Input
- Reduziert Abhängikeit von vorigen Layern
\text{Loss} + \beta \sum_{i=1}^{n} |\theta_i|
\text{Loss} + \beta \sum_{i=1}^{n} \theta_i^2
l1_regularization_loss = torch.norm(model.parameters(), 1)optimizer = torch.optim.Adam(model.parameters(), lr=lr, weight_decay=beta)
nn.Dropout(0.2) # 0.2 of neurons set to 0nn.BatchNorm1d()PyTorch
Regularisieren
- L1 (Lasso):
- kleine Parameter
- Gewichte -> 0 => Feature Auswahl
- L2 (Ridge):
- kleine, ausgeglichene Parameter
- meistgebrauchte regularisation
- Dropout: setzt zufällig Neuronen auf 0
- Modell redundant & robust
- Modell redundant & robust
- Batch Normalization: Normalisiert Layer Input
- Reduziert Abhängikeit von vorigen Layern
\text{Loss} + \beta \sum_{i=1}^{n} |\theta_i|
\text{Loss} + \beta \sum_{i=1}^{n} \theta_i^2
Dense(N, kernel_regularizer=keras.regularizers.l2(beta), bias_regularizer=keras.regularizers.l2(beta))
tf.keras.layers.Dropout(0.2) # 0.2 of neurons set to 0tf.keras.layers.BatchNormalization(),Dense(N, kernel_regularizer=keras.regularizers.l1(beta), bias_regularizer=keras.regularizers.l1(beta))
TensorFlow
Data Augmentation
- Mehr Daten -> grössere Modelle -> komplexere Aufgaben
Data Augmentation
- Mehr Daten -> grössere Modelle -> komplexere Aufgaben
- Mehr Daten durch Datenbearbeitung

Data Augmentation
- Mehr Daten -> grössere Modelle -> komplexere Aufgaben
- Mehr Daten durch Datenbearbeitung

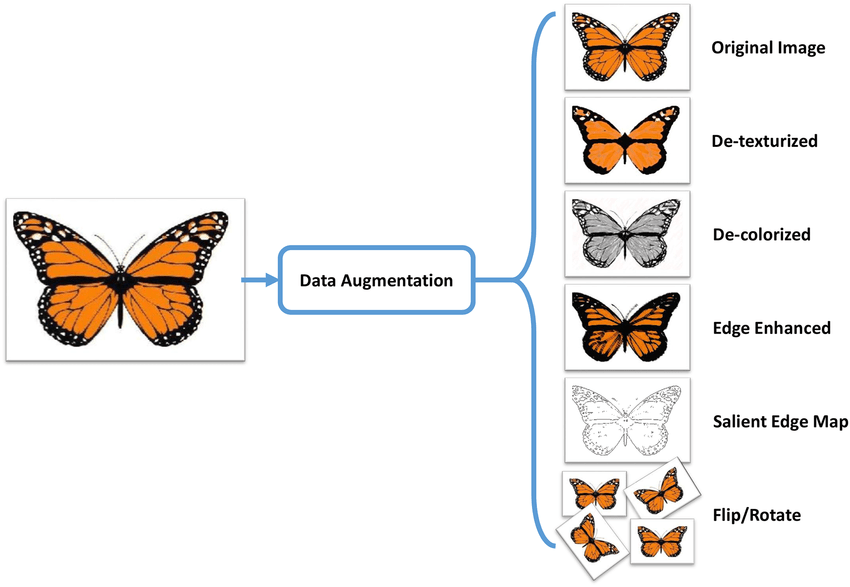
Data Augmentation
- Mehr Daten -> grössere Modelle -> komplexere Aufgaben
- Mehr Daten durch Datenbearbeitung


Data Augmentation
- Mehr Daten -> grössere Modelle -> komplexere Aufgaben
- Mehr Daten durch Datenbearbeitung
- Verbessert Generalisierung
- Reduziert Overfitting


Regularisieren
Hands-On: MNIST Classifier
Bearbeiten Sie dieses Notebook
- Modifizieren Sie den MNIST Classifier
mit zwei Regularisierungen: Dropout & L2
- Vergleichen Sie die Performance
mit und ohne Regularisierung
Die Lösung finden Sie in diesem Notebook